BQ 3 unit T

a. In our trig identities tangent relates to sin and cos in the ratio of tan=sin/cos. With the ratio the asymptotes and where the tangent graph is negative or positive can be explained. Asymptotes happen when the value of the graph is undefined and the only time the value for tan is undefined is when cos is equal to zero. So in turn the asymptotes of a tan graph are located where the relating cos graph touches the x axis. Tan= sin/cos also explains when tan is below or above the x axis. In the first quadrant both sin and cos are positive making the tan graph positive. In the second quadrant sin is positive but cos in negative so tan is negative. In the 3rd quadrant both sin and cos are negative making tan positive and in the 4th quadrant sin is negative but cos is positive so again tan is negative.

b. Cotangent is very similar to tangent the only difference being that cot=cos/sin instead of sin/cos. Because of this the asymptotes of a cot graph will differ from those of a tan graph. Instead of the asymptotes being where cos is zero the asymptotes will be where sin is zero shifting the asymptotes and the overall look of the graph. However whether cot is above or below the x axis stays consistent with tan graphs.

c. Secant graphs are closely related to cosine graphs. In regards to trig ratios sec=1/cos. So with that knowledge the asymptotes of a sec graph will be wherever cos=0. Sec graphs will follow the same positive and negative pattern as a cos graph and will be graphed accordingly, the only difference being that sec graphs are essentially a series of asymptotes.

d. Cosecant graphs are similar to secant graphs except the trig ratio for csc is 1/sin instead of 1/cos. Because of this the asymptotes are found wherever the related sin graph touches the x axis. Csc graphs also follow the same positive negative pattern of a sin graph and once again csc graphs are a series of parabolas.

Reflection #1 Unit Q- verifying trig identities.

1. Verifying a trig identity means using the various ratio and Pythagorean identities in order to simplify long and complicated problems with carious trig functions into something as simple as sin(x). It also means verifying that two different trig ratios are equal to each other which again means simplifying. So all in all verifying trig identities mainly means to simplify big long complicated problems into simple trig functions that are easy to work with.
2. There aren't many tips and tricks to solving these identities. One of the main tips I have is to get everything into related trig functions in order to be able to use a identity. Also you should probably never square both sides because itll make the problem more complicated than it already is.
3. The first thing I do is see if the trig functions currently relate to each other. If they do I look at the multiple possible path and choose the easiest one. After that i keep going using multiple trig identities or factoring along the way if i can. When its to verify I do it until i get both sides equal to each other. When its to simplify I go until there is hopefully just one trig function left

SP7- Unit Q concept 7- finding all trig functions

The biggest thing that needs to be understood is what identities to use. You need an identity that will get you to the information you need but there are usually multiple paths that can be taken. However it doesn't really matter which path is taken because in the end the answers will be the same although the difficulty may be greater for some paths when compared to others.

WPP 13/14 Unit P concepts 6/7

This WPP was made in collaboration with Tommy and William please visit the other awesome posts on their blogs by going here and here'
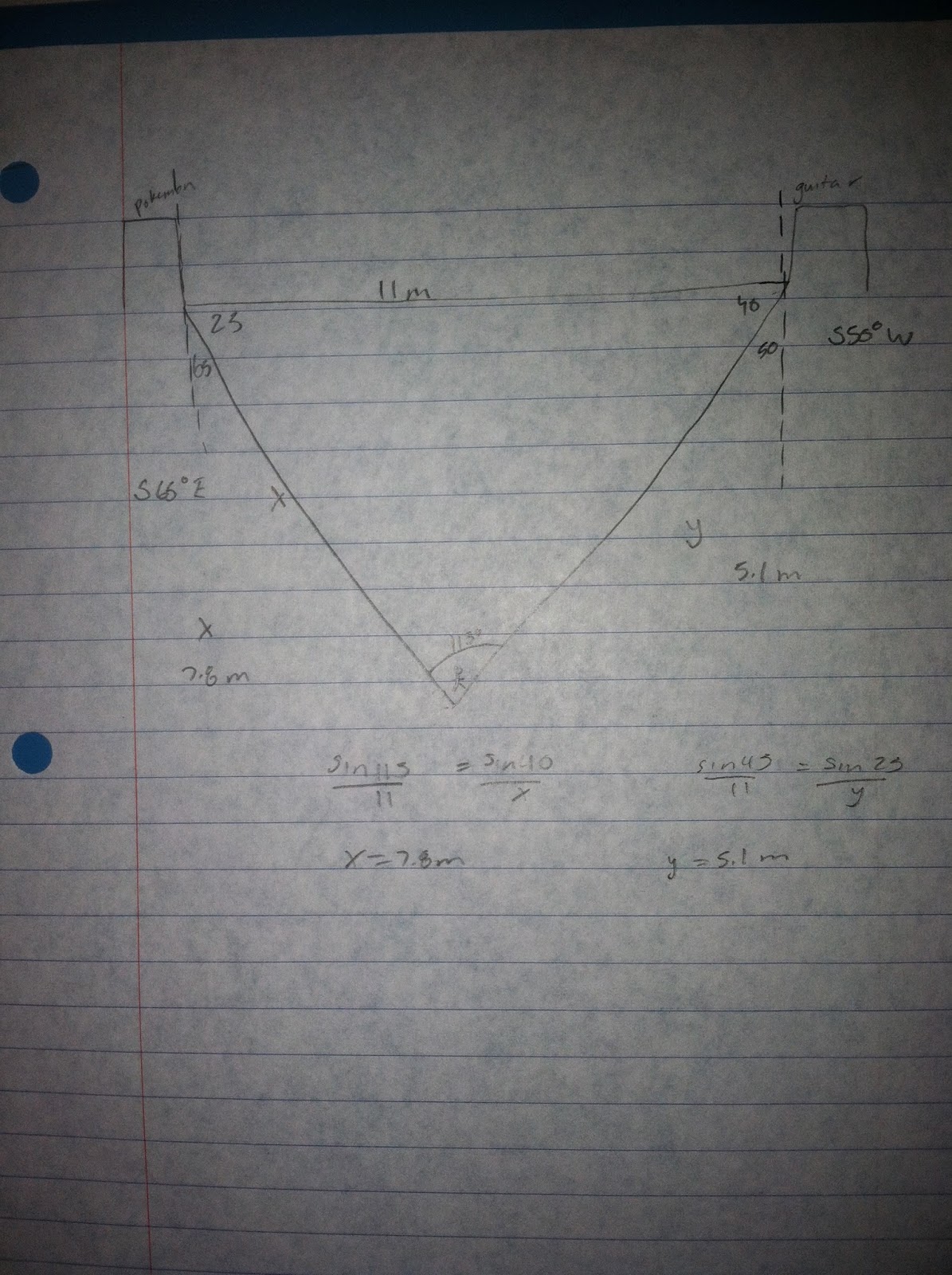
1. The Ups delivery man needs to make a delivery to Bobs pokemon store as well as Marty's guitar store. The stores are 11 miles apart from each other. The guitar store is S50W from the ups guy and the Pokemon store is S65 E form the ups guy. Find which store is closer to the ups guy.

The guitar store seems to be close at just 5.1 miles away.

2.Marty is sitting in his treehouse, He needs to go to both target and walmart. Target is 6 miles away at a bearing of 310. Walmart is 3 miles away ay 035. How far is Walmart from Target.

3. Bob is taking a break from his pokemon store. He goes to a river and sees a tree with delicious fruit on the the other side. He starts at point A and walks due south for 10 miles to point B. At point A there was a  bearing of S49W and at point B it was N62W. How far is the tree from point B.

BQ 1 Unit P

1. Law of sines: The main reason we need law of sines is to find unknown parts of a non right triangle. How ever in order to use law of sines we must be given either AAS, ASA or SSA.


                                                 http://www.youtube.com/watch?v=gAX_IleqeJQ
 As shown on the video we start with a triangle labeled ACB. We must drop a line from angle C in order to make 2 right triangles. From there we can figure out that the sin of a=h/b. Also that the sin of C=h/a. Then if you divide by ab you get sinA/a= sinC/c with is the law of sines.

4. This video will go over how the area of an oblique triangle is derived.

                  http://www.youtube.com/watchv=H8NEjzbvB6M#aid=P9gOqbIj4Vw
Our regular formula is area=1/2*bh. The new area formula is a=1/2*b(asinC) They relate because essentially they are the same formula the only difference is that we have solved and substituted for h. When we made the oblique triangle into a right triangle we used our knowledge of trig functions to find the h=asinC. This then goes into our normal formula giving us our new formula that now works for all triangles.

WPP #12 Unit O concept 10

http://commons.wikimedia.org/wiki/File:Looking_Up_at_Empire_State_Building.JPG

Bob has recently added a couple stories to his pokemon card shop but he has no idea how tall is new store really is and would really like to know. If Bob is standing 15 feet away and looking up at a 76 degree angle how tall is his store.

Now that Bob has found out how tall his newly improved store is he wants to know know how far the rival card shop is that is down the same perfectly level street that his card shop is on. He's standing on his 60.16 ft tall building looking down at a 33 degree angle.

I/D 2 unit O-how can we derive our patterns for the special right triangles

Inquiry Activity Summary

1.                                                               

We first start out with an equilateral triangle with each side length being 1. Since it is equilateral it is also equilateral so each angle measure is 60 degrees.

In order to create a 30 degree angle to give us our 30-60-90 triangle we must cut straight down splitting the 60 degree angle into two 30 degree angles while also creating a right angle with the base of the triangle.

When you cut an angle in half you also cut the side across from the angle in half. Since all the sides of the triangle started out as 1 when you cut it in half the side across form the 30 degree angle is now 1/2. So far we have the hypotenuse being unchanged and staying at 1 and the base or the side across from the 30 degree angle being cut in half into 1/2

Now that we have 2 of the three side we can now use the pythagorean theorem to solve for the 3rd side. The side across form the 30 will be a the side across from the 60 will be b and the hypotenuse will of course be c. We then plug those values into the formula and then square them. We end up with 1/4+b^2=1. From there we solve for b and end up with rad3/2 for our third side across from the 60 degree angle.

Now that we have each side of the triangle we can get rid of the fractions by multiplying each side by 2. 

By multiplying each side by 2 we get 1 rad3 and 2. This is very similar to our pattern of n n-rad3 and 2n. The only reason we have n instead of one is for it to be a generalization of the pattern for any number instead of just 1

2.

We first start with a square where all the side are equal to 1

From there we cut it diagonally in order to split the right angles and create 4 45 degree angles or two 45-45-90 triangles. Unlike the 30-60-90 triangle the sides stay unchanged at 1 since it was a diagonal cut.

We have the side across from the 2 45 degree angles and we are missing the hypotenuse. Since we have 2 sides and are missing one we can again use pythagorean theorem to find the last side. The work is shown in the picture and we end up finding out that the hypotenuse is equal to rad2

The sides of the triangle are 1 and 1 being the two legs and rad2 being the hypotenuse. This already looks very similar to our pattern and needs nothing done to it except for changing the 1's to n's to create a generalization for any number to fit in its place.

Inquiry Activity Reflection

Something i never noticed about the special right triangles is that they are derived from a square and a equilateral triangle.

Being able to derive these patterns myself aids in my learning because I now have a better understanding of the triangles now that I know where the pattern comes from and just in case i completely forget the pattern i could also just derive the two triangles from the square and the triangle.