BQ #3 unit T concepts 1-3

 How do the graphs of sin and cos relate to each of the others?

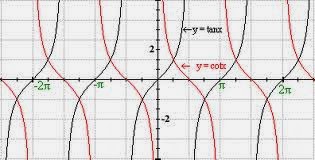
tangent?

      The trig ratio for tangent is sin/cos. Because of this the asymptote for tan can be found whenever cos is equal to zero. When cos is equal to zero the ratio of sin over cos which is equal to tan would be undefined creating and asymptote.

cotangent?

       The trig ratio for cot is cos/sin. Because of this the asymptote for cot can be found whenever sin is equal to zero. When sin is equal to zero cot would be equal to cos/0 and that would be undefined since you cant divide by a zero. An undefined section of the graph will create an asymptote.
secant?

        The trig ratio for sec is 1/cos. Whenever cos is equal to zero sec will be undefined which will create an asymptote. So whenever cos is equal to zero a sec graph will have as asymptote. Sec is also the inverse of cos so the sec graph will stem off from cos graph.
cosecant?

       The trig ratio for csc is 1/sin. This means that whenever sin is equal to zero the related csc graph will have an asymptote. Since csc is the inverse of sin, csc graphs will stem off from the corresponding sin graphs 

BQ #2 Unit T concept: intro

How do trig graphs relate to the unit circle?

Period? - Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

The period for sin and cos is 2pi because of the patterns they follow on the unit cirlce. Sin follows a ++-- pattern and cos follows a -++- pattern. It takes one full unit circle in order for the pattern to repeat for sin and cos and one full unit circle has a length of 2pi. Since a period is how long the graph takes to reach the point it started it will take a length of 2pi because that's how long it takes the patterns for sin and cos to repeat themselves. The period for tan and cot are both just pi units long. This is because the unit circle pattern for tan and cot is +-+-. Because of that pattern it takes only half the distance of the unit cirlce to repeat itself. Half the distance of the unit circle would be pi, making the period for tan and cot just pi.

Amplitude? – How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?

sin

 

For trig functions only only sin and cos have amplitudes because of they behave on the unit circle. The limits of a cos on the unit circle are found at 1,0 and -1,0. The +1 and -1 look very familiar. That's because the amplitude of a cos graph is alos equal to one. Since the limits of cos are at those coordinates that has to also be the limits of a cos graph. Since 1,0 is the start and end of a the unit circle that's why cos starts and ends at 1. The same goes for sin only sins limits are found at 0,1 and 0,-1. Since the limits are again at 1 and -1 on the unit circle the same must be the same for the trig graphs.

BQ #4 Unit T

Why is tangent uphill and cotangent down hill?

As you can see tan and cot have their asymptotes in different places which affects how they are drawn. However they both follow the same positive negative pattern according to the unit circle. Since tan has an asymptote at pi where tan is positive the graph must follow close to the asymptote without reaching the x axis which it can only active by going towards positive infinite but then the same graph has to be negative in the next quadrant over with the asymptote being at 2pi so the graph would have to reach towards negative infinity while going along the asymptote. Because of this the tan graph must go follow that shape. The same goes for cot but since the asymptotes are in different places in relation to the positive negative pattern the graph must go towards negative infinity along the first asymptote and towards positive infinity along the second asymptote which will give it the shape it has.

BQ 3 unit T

a. In our trig identities tangent relates to sin and cos in the ratio of tan=sin/cos. With the ratio the asymptotes and where the tangent graph is negative or positive can be explained. Asymptotes happen when the value of the graph is undefined and the only time the value for tan is undefined is when cos is equal to zero. So in turn the asymptotes of a tan graph are located where the relating cos graph touches the x axis. Tan= sin/cos also explains when tan is below or above the x axis. In the first quadrant both sin and cos are positive making the tan graph positive. In the second quadrant sin is positive but cos in negative so tan is negative. In the 3rd quadrant both sin and cos are negative making tan positive and in the 4th quadrant sin is negative but cos is positive so again tan is negative.

b. Cotangent is very similar to tangent the only difference being that cot=cos/sin instead of sin/cos. Because of this the asymptotes of a cot graph will differ from those of a tan graph. Instead of the asymptotes being where cos is zero the asymptotes will be where sin is zero shifting the asymptotes and the overall look of the graph. However whether cot is above or below the x axis stays consistent with tan graphs.

c. Secant graphs are closely related to cosine graphs. In regards to trig ratios sec=1/cos. So with that knowledge the asymptotes of a sec graph will be wherever cos=0. Sec graphs will follow the same positive and negative pattern as a cos graph and will be graphed accordingly, the only difference being that sec graphs are essentially a series of asymptotes.

d. Cosecant graphs are similar to secant graphs except the trig ratio for csc is 1/sin instead of 1/cos. Because of this the asymptotes are found wherever the related sin graph touches the x axis. Csc graphs also follow the same positive negative pattern of a sin graph and once again csc graphs are a series of parabolas.

Reflection #1 Unit Q- verifying trig identities.

1. Verifying a trig identity means using the various ratio and Pythagorean identities in order to simplify long and complicated problems with carious trig functions into something as simple as sin(x). It also means verifying that two different trig ratios are equal to each other which again means simplifying. So all in all verifying trig identities mainly means to simplify big long complicated problems into simple trig functions that are easy to work with.
2. There aren't many tips and tricks to solving these identities. One of the main tips I have is to get everything into related trig functions in order to be able to use a identity. Also you should probably never square both sides because itll make the problem more complicated than it already is.
3. The first thing I do is see if the trig functions currently relate to each other. If they do I look at the multiple possible path and choose the easiest one. After that i keep going using multiple trig identities or factoring along the way if i can. When its to verify I do it until i get both sides equal to each other. When its to simplify I go until there is hopefully just one trig function left

SP7- Unit Q concept 7- finding all trig functions

The biggest thing that needs to be understood is what identities to use. You need an identity that will get you to the information you need but there are usually multiple paths that can be taken. However it doesn't really matter which path is taken because in the end the answers will be the same although the difficulty may be greater for some paths when compared to others.

WPP 13/14 Unit P concepts 6/7

This WPP was made in collaboration with Tommy and William please visit the other awesome posts on their blogs by going here and here'
1. The Ups delivery man needs to make a delivery to Bobs pokemon store as well as Marty's guitar store. The stores are 11 miles apart from each other. The guitar store is S50W from the ups guy and the Pokemon store is S65 E form the ups guy. Find which store is closer to the ups guy.

The guitar store seems to be close at just 5.1 miles away.

2.Marty is sitting in his treehouse, He needs to go to both target and walmart. Target is 6 miles away at a bearing of 310. Walmart is 3 miles away ay 035. How far is Walmart from Target.

3. Bob is taking a break from his pokemon store. He goes to a river and sees a tree with delicious fruit on the the other side. He starts at point A and walks due south for 10 miles to point B. At point A there was a  bearing of S49W and at point B it was N62W. How far is the tree from point B.