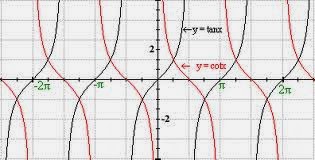
As you can see tan and cot have their asymptotes in different places which affects how they are drawn. However they both follow the same positive negative pattern according to the unit circle. Since tan has an asymptote at pi where tan is positive the graph must follow close to the asymptote without reaching the x axis which it can only active by going towards positive infinite but then the same graph has to be negative in the next quadrant over with the asymptote being at 2pi so the graph would have to reach towards negative infinity while going along the asymptote. Because of this the tan graph must go follow that shape. The same goes for cot but since the asymptotes are in different places in relation to the positive negative pattern the graph must go towards negative infinity along the first asymptote and towards positive infinity along the second asymptote which will give it the shape it has.
Tuesday, April 22, 2014
Monday, April 21, 2014
BQ 3 unit T
a. In our trig identities tangent relates to sin and cos in the ratio of tan=sin/cos. With the ratio the asymptotes and where the tangent graph is negative or positive can be explained. Asymptotes happen when the value of the graph is undefined and the only time the value for tan is undefined is when cos is equal to zero. So in turn the asymptotes of a tan graph are located where the relating cos graph touches the x axis. Tan= sin/cos also explains when tan is below or above the x axis. In the first quadrant both sin and cos are positive making the tan graph positive. In the second quadrant sin is positive but cos in negative so tan is negative. In the 3rd quadrant both sin and cos are negative making tan positive and in the 4th quadrant sin is negative but cos is positive so again tan is negative.
b. Cotangent is very similar to tangent the only difference being that cot=cos/sin instead of sin/cos. Because of this the asymptotes of a cot graph will differ from those of a tan graph. Instead of the asymptotes being where cos is zero the asymptotes will be where sin is zero shifting the asymptotes and the overall look of the graph. However whether cot is above or below the x axis stays consistent with tan graphs.
c. Secant graphs are closely related to cosine graphs. In regards to trig ratios sec=1/cos. So with that knowledge the asymptotes of a sec graph will be wherever cos=0. Sec graphs will follow the same positive and negative pattern as a cos graph and will be graphed accordingly, the only difference being that sec graphs are essentially a series of asymptotes.
d. Cosecant graphs are similar to secant graphs except the trig ratio for csc is 1/sin instead of 1/cos. Because of this the asymptotes are found wherever the related sin graph touches the x axis. Csc graphs also follow the same positive negative pattern of a sin graph and once again csc graphs are a series of parabolas.
b. Cotangent is very similar to tangent the only difference being that cot=cos/sin instead of sin/cos. Because of this the asymptotes of a cot graph will differ from those of a tan graph. Instead of the asymptotes being where cos is zero the asymptotes will be where sin is zero shifting the asymptotes and the overall look of the graph. However whether cot is above or below the x axis stays consistent with tan graphs.
c. Secant graphs are closely related to cosine graphs. In regards to trig ratios sec=1/cos. So with that knowledge the asymptotes of a sec graph will be wherever cos=0. Sec graphs will follow the same positive and negative pattern as a cos graph and will be graphed accordingly, the only difference being that sec graphs are essentially a series of asymptotes.
d. Cosecant graphs are similar to secant graphs except the trig ratio for csc is 1/sin instead of 1/cos. Because of this the asymptotes are found wherever the related sin graph touches the x axis. Csc graphs also follow the same positive negative pattern of a sin graph and once again csc graphs are a series of parabolas.
Friday, April 4, 2014
Reflection #1 Unit Q- verifying trig identities.
1. Verifying a trig identity means using the various ratio and Pythagorean identities in order to simplify long and complicated problems with carious trig functions into something as simple as sin(x). It also means verifying that two different trig ratios are equal to each other which again means simplifying. So all in all verifying trig identities mainly means to simplify big long complicated problems into simple trig functions that are easy to work with.
2. There aren't many tips and tricks to solving these identities. One of the main tips I have is to get everything into related trig functions in order to be able to use a identity. Also you should probably never square both sides because itll make the problem more complicated than it already is.
3. The first thing I do is see if the trig functions currently relate to each other. If they do I look at the multiple possible path and choose the easiest one. After that i keep going using multiple trig identities or factoring along the way if i can. When its to verify I do it until i get both sides equal to each other. When its to simplify I go until there is hopefully just one trig function left
2. There aren't many tips and tricks to solving these identities. One of the main tips I have is to get everything into related trig functions in order to be able to use a identity. Also you should probably never square both sides because itll make the problem more complicated than it already is.
3. The first thing I do is see if the trig functions currently relate to each other. If they do I look at the multiple possible path and choose the easiest one. After that i keep going using multiple trig identities or factoring along the way if i can. When its to verify I do it until i get both sides equal to each other. When its to simplify I go until there is hopefully just one trig function left
Subscribe to:
Posts (Atom)